Solving In-order Successor Coding Problem
Problem statement
Write an algorithm to find the "next" node (i .e., in-order successor) of a given node in a binary search tree. You may assume that each node has a link to its parent.
To solve the above problem first let's understand what's a binary tree, binary search tree, and in-order successor.
Binary Tree
A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.
Here is how we can define a binary tree node:
class BinaryTreeNode {
value = null;
left = null;
right = null;
constructor(v) {
this.value = v;
}
}Binary Search Tree
Binary Search Tree is a node-based binary tree data structure that has the following properties:
- The left subtree of a node contains only nodes with values lesser than the node’s value.
- The right subtree of a node contains only nodes with values greater than the node’s value.
- Each left and right subtree must follow #1 and #2 properties.
In-order Successor
The next node in the Inorder traversal of the binary tree calls an in-order successor. In inorder traversal, we first traverse the left node, then the root node, and then the right node.
To solve the problem if we need a reference to the parent node as it would require traversing in up direction in the tree with each subtree traversing.
We can modify BinaryTreeNode to use solving the problem. We are adding a parent property.
class BinaryTreeNode {
value = null;
left = null;
right = null;
parent = null;
constructor(v) {
this.value = v;
}
}There are two traversal approaches we would use to solve the problem.
Right and Left Node Traversal
A node's right child will have a higher value than the node's value, so if a node has a right child, then first we need to traverse the right and left most node in the left subtree.
Parent Node Traversal
When a node does not have a right node, then we traverse up to find the higher value.
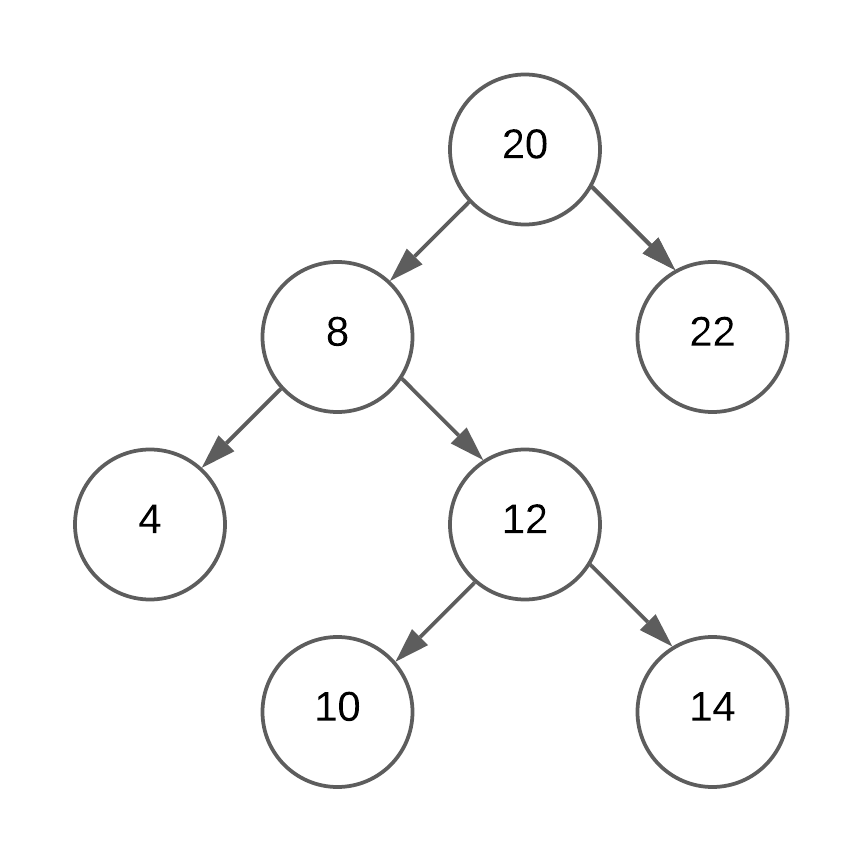
We have used the same example of the binary search tree in our source code as shown in the above picture.
The in-order successor for 8 is 10, for 14 it's 20 and for 22 it's null.
Here is the complete source code to solve the problem:
function print() {
console.log(JSON.stringify(arguments, null, 4));
}
class BinaryTreeNode {
value = null;
left = null;
right = null;
parent = null;
constructor(v) {
this.value = v;
}
}
const n1 = new BinaryTreeNode(22);
const n2 = new BinaryTreeNode(20);
const n3 = new BinaryTreeNode(14);
const n4 = new BinaryTreeNode(12);
const n5 = new BinaryTreeNode(10);
const n6 = new BinaryTreeNode(8);
const n7 = new BinaryTreeNode(4);
n2.right = n1;
n2.left = n6;
n6.left = n7;
n6.right = n4;
n4.left = n5;
n4.right = n3;
n1.parent = n2;
n3.parent = n4;
n4.parent = n6;
n5.parent = n4;
n6.parent = n2;
n7.parent = n6;
function getLeftMostNodeValue(node) {
if (!node.left) {
return node.value;
}
return getLeftMostNodeValue(node.left);
}
function getParentHighNodeValue(node, v) {
if (!node) {
return null;
}
if (node.value > v) {
return node.value;
}
return getParentHighNodeValue(node.parent, v);
}
function inOrderSuccessor(node) {
if (!node) {
return null;
}
if (node.right) {
return getLeftMostNodeValue(node.right);
} else {
return getParentHighNodeValue(node.parent, node.value);
}
}
print("inOrderSuccessor", inOrderSuccessor(n6) === 10);
print("inOrderSuccessor", inOrderSuccessor(n3) ===20);
print("inOrderSuccessor", inOrderSuccessor(n1) === null);
print("inOrderSuccessor", inOrderSuccessor(n5) === 12);Time Complexity
In a worst-case scenario, the above solution would traverse each node once, so the time complexity is O(N).
Space Complexity
As we have used recursive function call, it would keep adding a call stack so the space complexity is O(N).